Ângulos na circunferência: ângulo excêntrico interno e externo

Atividades (8)

Navegue ao lado nos tipo de atividade para visualizar as propostas para essa aula.

1. 1. Questão de múltipla escolha:

   

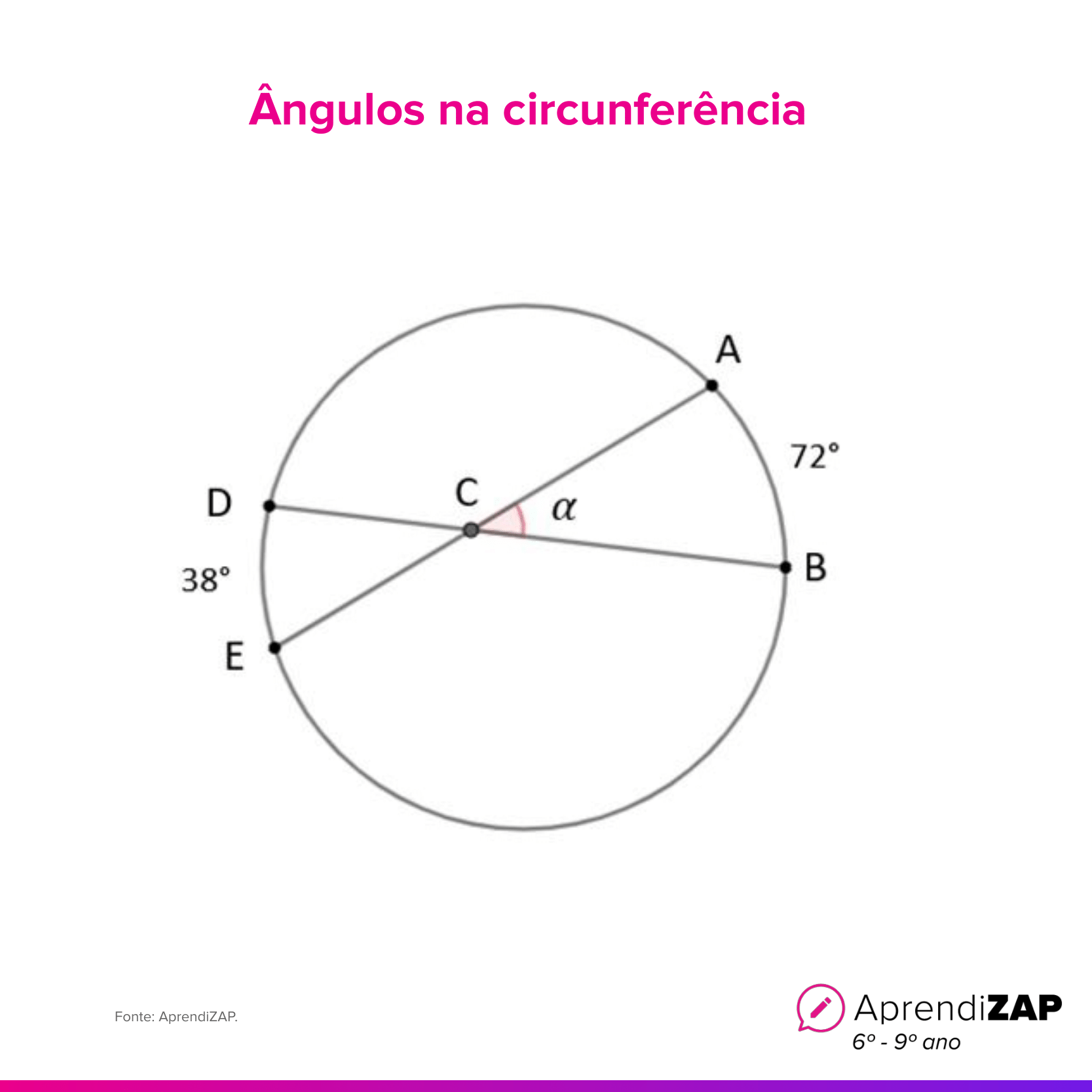
   Sabendo que C não é o centro da circunferência, determine o valor do ângulo α:

   A)

   O ângulo 𝜶 mede 55°

   B)

   O ângulo 𝛼 mede 72°

   C)

   O ângulo 𝛼 mede 110°

   Atividade completa

   ---

2. 2. Atividade aberta:

   
   Atividade completa

   ---

3. 3. Design Sprint:

   

   O objetivo aqui é que os alunos aprendam sobre ângulos na circunferência, mais especificamente sobre ângulo excêntrico interno e externo. Esses conceitos são importantes para entender a relação entre arcos, ângulos centrais e ângulos inscritos na circunferência. Além disso, os alunos poderão aplicar esses conceitos em situações cotidianas, como em projetos de arquitetura, na construção de objetos circulares, em jogos de tabuleiro, entre outros.

   Atividade completa

   ---

4. 4. Sala de Aula Invertida:

   

   O objetivo aqui é trabalhar com ângulos na circunferência, mais especificamente, ângulo excêntrico interno e externo. Esses conceitos são importantes para entendermos como os ângulos se relacionam com a circunferência e como podemos utilizá-los para resolver problemas. Para contextualizar o tema, podemos citar exemplos como a construção de rodas de bicicleta, que precisam de medidas precisas para garantir o bom funcionamento, ou a construção de pontes, que também requerem cálculos precisos para garantir a segurança.

   Atividade completa

   ---

5. 5. Rotação por estações:

   

   Os ângulos na circunferência são fundamentais para a compreensão da geometria e da trigonometria. Eles estão presentes em diversas situações do cotidiano, como na construção de rodas de bicicleta, na medição de ângulos em mapas e na criação de objetos circulares. O objetivo aqui é que os alunos aprendam sobre ângulos excêntricos internos e externos na circunferência, e como eles podem ser utilizados para resolver problemas.

   Atividade completa

   ---

6. 6. Ensino Híbrido:

   

   O objetivo aqui é aprender sobre ângulos na circunferência, mais especificamente sobre ângulo excêntrico interno e externo. Esses conceitos são importantes para entendermos como os ângulos se relacionam com a circunferência e como podemos utilizá-los para resolver problemas. Para tornar a aula mais envolvente e didática, é importante utilizar exemplos práticos e contextualizados que possam ser aplicados no cotidiano dos estudantes.

   Atividade completa

   ---

7. 7. Estudo de Caso:

   

   O objetivo aqui é que os alunos aprendam sobre ângulos na circunferência, mais especificamente sobre ângulo excêntrico interno e externo. Esses conceitos são importantes para entender a relação entre arcos, ângulos centrais e ângulos inscritos na circunferência. Além disso, os alunos poderão aplicar esses conceitos em situações cotidianas, como em cálculos de medidas de peças circulares em uma fábrica ou em projetos de arquitetura.

   Atividade completa

   ---

8. 8. Design Thinking:

   

   O objetivo aqui é trabalhar sobre ângulos na circunferência, mais especificamente sobre ângulo excêntrico interno e externo. Esses conceitos são importantes para entendermos como os ângulos se relacionam com a circunferência e como podemos utilizá-los em problemas de geometria. Para contextualizar, é importante citar exemplos como a construção de rodas de bicicleta, que utilizam ângulos na circunferência para garantir a estabilidade e segurança do ciclista.

   Atividade completa

   ---